
If you just want the answer, then here it is: 142 masks. How do I know? Read on!
Consider for a moment not 36 masks but 4. You can think of the Red Hau, Green Miru, White Akaku, and Black Pakari if you wish, but I am just going to number them: 0, 1, 2, and 3. (Why not 1, 2, 3, 4? You will see later.) Now imagine that you have a magic bucket with an infinite supply of randomly distributed masks. You cant see into the bucket, and you can only take out one mask at a time. You want to collect all four masks. How many masks will you have to take out of the bucket?
The smallest number of masks you may need to take out is four: one of each mask. The largest number of masks you may need to take out is infinite. You may never complete that set! Your experience will most likely fall between those two extremes, and that is where probability comes in.
How likely are you to complete your set of four in just four tries? Consider thousands of people each reaching into their magic buckets and pulling out just four masks, one after the other. They each keep track of not only what they pulled out, but also what order they pulled them out. You might see runs like these:
3310
2122
0000
or even
They are each as likely as the other to occur! At first glance, 0000 and 0123 dont seem to be as likely as the others, but they are. They each occur just once in the set of all possible outcomes.
They do however belong to small subsets of the overall set of all possible outcomes. 0000 consists of all the same mask, and 0123 is a complete set. 0120, 3310, and 2122 are all members of larger subsets, and because their subsets are larger, the numbers seem less special.
Those of you familiar with Base N arithmetic know that there are 4 4 = 256 possible ways to draw four masks from our magic bucket. They can be enumerated this way:
0001
0002
0003
0010
0011
3330
3331
3332
3333
If you are unfamiliar with Base N arithmetic, then think about taking out just two masks from a magic bucket with an infinite supply of ten different types (0, 1, 2, , 9) of mask in it. Ten different masks give you normal Base 10 arithmetic. The possibilities range from 00, 01, 02, 03, all the way up to 97, 98, and 99. All totaled, that is 10 2 = 100 possibilities. (Do you see why we started with 0 instead of 1?)
Back to our four masks: if half of all the possible outcomes contained 0s and or 1s (which they do), then we say there is a 50/50 chance of you pulling out a 0 mask, 1 mask, or both. We are interested in those outcomes where we have a complete set. Those outcomes are: 0123, 0213, 0231, , 3201, 3210 (i.e. all possible permutations of 0, 1, 2, and 3). In this limited case, it is easy to determine how many permutations are complete sets: 4 x 3 x 2 x 1 = 4! = 24. (The notation 4! is read four factorial.) So the odds of a complete collection of four unique masks when you draw only four masks is 24/256 = 0.09375, or just over nine percent of the time.
From this it is very easy to extrapolate and determine the odds of getting all 36 unique KANOHI NUVA when purchasing just that many masks (i.e. 18 boxes):
That is about one chance in 300 trillion (300 billion for you people on the British system). In other words, it is not going to happen.
The situation becomes more complicated when you start pulling out more masks than what you are looking for. Consider drawing five masks from our magic bucket of four types of masks. The total number of ways you can draw masks is now 4 5 (= unique masks masks drawn ) or 1024 ways. Now consider all of those times we draw five masks, but never get a 3 (01201, 01202, 22011, etc.). There are 3 5 such possibilities.
How about those times we dont get a 2? (01301, 01303, 33011, etc.). Again, there are 3 5 such possibilities. We have just substituted 2 for 3. It should be obvious that we can do the same thing with 0 and 1 for a total of 4 x 3 5 = 972 ways we dont get a complete set.
But wait! We have made a mistake! Consider the draw 01010. It does not have a 3, so we counted it as a number without a 3. But it also does not have a 2, so we also counted it as a number without a 2. We double counted 01010, so we have to add one of those back in. In fact, we double counted for all six combinations of two [(0,1), (0,2), (0,3), (1,2), (1,3), and (2,3)]. The number of numbers like this that we need to add back is 6 x 2 5 = 192.
But wait! We made another mistake! Consider the draw 00000. It does not have a 1 or a 2 or a 3, so we took it out three times. But it also does not have the combinations (1,2), (1,3), or (2,3), so we put it back in three times too. That is one time too many. It is clearly not a complete set, so we have to take it out one more time. The same goes for 11111, 22222, and 33333. That is 4 times total.
So the total number of complete sets, S , in draws of five masks is:
This result generalizes to the following for draws of n masks:
For n = five, 240 complete sets out of 1024 possible sets is slightly worse than one chance in four. But for n = seven, 8400 complete sets out of 16384 possible sets is a chance slightly better than 50/50.
[Exercise for the reader. Check S = 4! for n = 4 and S = 0 for 0 n
It only takes a little thought and/or experimentation with numbers of unique masks other than four to determine that the number of complete sets is a power series of the form:
where m is the number of unique masks in a complete set, n is the number of masks pulled from the magic bucket, and
is the number of combinations of m unique masks taken k at a time. For the KANOHI NUVA ( m = 36), this is:
Dont go plugging that formula into your calculator. Most calculators cant handle numbers 1 x 10 100 and beyond, and the numbers we are talking about here go up to almost 1 x 10 221 . Even a spreadsheet like Excel does not have the necessary precision to calculate the values exactly. You need Mathematica® or some other program capable of doing symbolic calculations (i.e. long-hand arithmetic) to accurately calculate these sums.
To determine your probability of getting a complete set, you need to divide S above by 36 n :
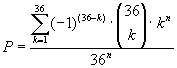
Armed with that equation and a program capable of calculating the result, you can easily discover that for n = 142: P = 0.5012 . Or in other words, just over 50% of the time you will have drawn a complete set by the 142 nd mask.
So, on to the experiment! What happens if I purchase 72 boxes (= 144 = 1 gross) of KANOHI NUVA? Keep in mind, we would have to repeat this experiment thousands of times to determine experimentally the validity of the above statistics. Essentially, I am flipping a coin once. Whether it comes up heads or tails the first time proves nothing.
Nevertheless, I was determined to try it. Here is what I received:
| White | Red | Brown | Blue | Green | Black | Totals | ||
| Akaku | 5 | 5 | 0 | 2 | 2 | 5 | 19 | |
| Hau | 8 | 3 | 5 | 3 | 4 | 5 | 28 | |
| Kakama | 7 | 1 | 2 | 3 | 6 | 3 | 22 | |
| Kaukau | 4 | 5 | 3 | 3 | 6 | 3 | 24 | |
| Miru | 2 | 8 | 3 | 0 | 1 | 7 | 21 | |
| Pakari | 9 | 5 | 5 | 6 | 3 | 2 | 30 | |
| Totals | 35 | 27 | 18 | 17 | 22 | 25 |
As you can see, I came up two masks short: the BROWN AKAKU NUVA and the BLUE MIRU NUVA. The odds of having at least two masks left after drawing 144 masks are about 1-in-6, so although the result was disappointing, it was not out of the question especially for someone with luck as bad as mine.
Items of note:
1) The 8598 boxes I received were all perforated like the original 8525 boxes.
2) My fourth and fifth boxes were identical: one GREEN HAU and one BLACK MIRU each.
3) My nineteen, twentieth, and twenty-first boxes completed the RED, WHITE, and BLACK color series, respectively.
4) Box number sixty-four contained two RED PAKARI.
Update: I audited my masks and discovered that I had mis-filed a few. I have since corrected the numbers above.
0 Comments